Planning for disaster
In times of disaster, we tend to call in force majeure on our projects, and therefore, keep our hands off. Stating no-one could foresee the possibility and impact of said force majeure, we cannot handle it within our project objectives of scope/time/cost. Both employer and contractor will take their responsibility and take a piece of the incurred damages. But can’t we plan for disaster? Are there established principles to do so?
As engineers we own a reflex of going into detail when modeling our projects to increase the confidence we have in the plan. We break up work into activities that we can estimate up to a level of great certainty. We even sometimes apply uncertainty and identified risk events onto this model and forcing statistics to do their part in assuring us and our stakeholders of the feasibility of our projects. We include the resulting known unknowns in our baseline as contingency reserves or buffers.
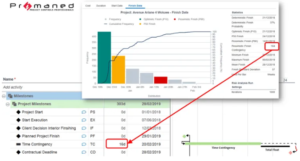
Fig. 01 – Calculated amount of contingency reserve needed to assure 90 % feasibility of the finish date of this project. Based on Monte Carlo simulations, using the risk and schedule data provided.
What we cannot model is a black swan [1]. An event that occurs with such a low probability and high impact, that we assume them nonexistent. However, we consider it an intelligent way of working to account for these unknown unknowns somewhere within our reserves. Thankfully, Project Controls principles hand us the technique to cope with black swans.
Management Reserve
In industrial environments with a lot of these black swan events, let’s say research and development, people account a certain reserve into their budget and time as a specific amount of management reserve (MR). This bucket of time and budget is assigned to a certain (set of) project(s). It’s reserved for anything we couldn’t have predicted. The parameters defining the amount of management reserve assigned to the (set of) project(s) can be various. Inclusion of more strategic values and risk appetite on those can be done through weighting the importance of each strategic value and multiplying by the presence of unknown unknowns.
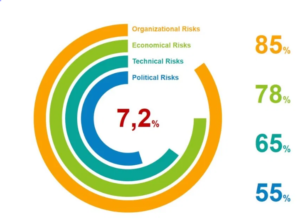
Fig. 02 – MR calculation based on external risk factors to the project we cannot objectively calculate. The risk appetite on each of these categories and the existence of unknown unknowns defines the assigned amount of MR at 7,1 %.
Management reserve is established, it’s accepted to be an agreed upon available amount but taken outside of the project’s objectives. It is thus not part of the baseline, which we use to track the project’s health. Consequently, MR can only be transferred to the budget baseline following strict baseline change management processes. This management reserve is calculated as an uncertainty percentage on the project budget and greatly makes use of the risk pooling effect.
The risk pooling effect is met when we take multiple objects into account that are object to risk and uncertainty. The amount needed to cover for the effect of an uncertainty occurring by 80% for the individual objects will always be greater than covering all events pooled together by 80%.
Contingency Reserve
The greatest distinction between management reserves and contingency reserves is the knowledge of the risk’s existence. Contingency reserves are established to cover for the known unknowns, the accepted project risk. It is calculated by statistical models like Monte Carlo Analysis, including the risk register that’s mapped onto the schedule. All this information is based on the project stakeholders’ knowledge and past experiences, something we cannot say about management reserve.
As professionals we must accept the existence of these unknown unknowns, not by actively scheduling for them, but by reserving some budget to cover for them, must they occur.
[1] Taleb, Nassim Nicholas, The Black Swan: The Impact of the Highly Improbable. Random House, New York (2007). ISBN 978-1400063512.



